Aproksymacja liczby π w Ruby

Dzień liczby pi już za nami. Jako programiści Ruby uważamy, że ludolfina (liczba π) zasługuje na więcej uwagi. Rok w rok dnia 22 lipca w Europie obchodzimy Dzień Aproksymacji Liczby π (Pi). U niektórych w głowach mogą pojawić się dwa pytania. Czym jest aproksymacja? Oraz dlaczego akurat dzień 22.07 jest Dniem Aproksymacji Liczby Pi?

Zacznijmy od tego, czym jest aproksymacja (łac. approximare – przybliżać)? Jest to sposób na znalezienie przybliżonego rozwiązania danego problemu. Aproksymację stosujemy kiedy nie można bezpośrednio uzyskać rozwiązania, a chcemy poznać najbliższą jego wartość tak jak to jest w przypadku liczby pi.

Dlaczego 22.07 został dniem aproksymacji liczby pi? Zawdzięczamy to wybitnemu uczonemu Archimedesowi. Niewątpliwie jest on uznawany za najwybitniejszego matematyka swoich czasów. To on jako pierwszy zajął się problemem aproksymacji liczby pi. Wykorzystał znaną sobie wiedzę matematyczną i wyliczył, że wartość π zawiera się między 223/71 (=> 3.140845), a 22/7 (=> 3.142857). A stąd już blisko do świętowania. 🎉 Posługując się europejskim zapisem dat otrzymujemy 22 lipca jako Dzień Aproksymacji Liczby Pi.

Archimedes i jego sposób na liczbę pi

Jak Archimedes przybliżył liczbę pi? Od wieków posiadano wiedzę, że stosunek obwodu (ang. circumference) koła do jego średnicy (ang. diameter) C/d jest stały. Ta stała wartość to właśnie π. Jeżeli rozważyć koło o średnicy 1 wtedy jego obwód będzie równy pi. To był punkt wyjścia. Następnie Archimedes zaczął wpisywać w koło oraz opisywać na nim wielokąty foremne. Obwód wielokąta wpisanego był mniejszy od obwodu koła (tym samym zawężał dolną granicę pi). Natomiast obwód wielokąta opisanego był większy (co wyznaczało górną granicę pi). W ten sposób wskazał przedział w jakim należy szukać pi. Przeprowadził pierwszą aproksymację tej liczby. Dokonując wyliczeń dla 96-kąta foremnego, udało mu się ustalić liczbę pi do dwóch miejsc po przecinku.

Dość długo ta metoda służyła do kolejnych wyliczeń π. Z czasem pojawiły się inne sposoby na aproksymację liczby pi. Zalicza się do nich aproksymację za pomocą ciągów nieskończonych. Poniżej kilka przykładów.

Viète i jego aproksymacja

Jako pierwszą aproksymację w Europie, przy użyciu ciągów nieskończonych, podaje się wzór Viète. Za jego pomocą udało się obliczyć pi do dziewięciu miejsc po przecinku. Można znaleźć jego dwa zapisy:

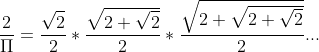
lub

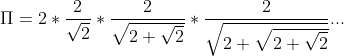
Nie bylibyśmy sobą gdybyśmy nie pokusili się o napisanie krótkiej metody w Ruby. 💎

def approximation_pi_with_viete_formula(n)
  factor = 2.0
  return factor if n == 0

  denominator = Math.sqrt(2)
  product = factor
  product *= factor / denominator
  return product if n == 1

  n.times do
    new_denominator = Math.sqrt(2 + denominator)
    product *= factor / new_denominator
    denominator = new_denominator
  end
  product
end

Wzór John’a Wallis’a

Jako drugą w Europie podaje się aproksymację John’a Wallis’a. Jest ona łatwa w zastosowaniu ponieważ opiera się na granicy ciągu liczb wymiernych. Wzór przedstawia się następująco:

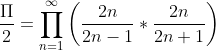
Dla naszych programistycznych potrzeb można przenieść 2 na drugą stronę równania.

def approximation_pi_with_wallis_formula(n)
  product = 1.0
  n.times do |k|
    counter = 2.0 * (k + 1)
    first_factor = counter / (counter - 1)
    second_factor = counter / (counter + 1)
    product *= first_factor * second_factor
  end
  2 * product
end

Aproksymacja Leibniz’a

Znana również pod dwoma innymi nazwami: Gregory - Leibniz lub Gregory - Leibniz - Madhava. Pozwala ona na wyznaczenie pi z dużą precyzją. Jest to jednak tak zwana “wolno zbieżna” metoda. Za jej pomocą należy wykonać zdecydowanie więcej obliczeń aby uzyskać wynik. Nakład pracy w obliczenia jest niesamowicie duży w porównaniu z innymi sposobami. Wzór na aproksymację Leibniz’a to:

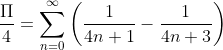
Jak może wyglądać przykładowa metoda dla tej aproksymacji?

def approximation_pi_with_leibniz_formula(n)
  4 * n.times.sum do |k|
    1.0 / (4 * k + 1) - 1.0 / (4 * k + 3)
  end
end

Tu również, dla czytelności uzyskanego wyniku, 4 można przenieść na drugą stronę równania.

Nilakantha i jego wzór

Swoje rozwiązanie przybliżenia wartości π zaprezentował indyjski astronom Nilakantha Somayaji. Aproksymacja Nilakantha okazała się szybciej zbieżna, a wzór ma postać:

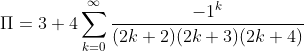
Jego implemetacja w Ruby może wyglądać następująco:

def approximation_pi_with_nilakantha_formula(n)
  one = -1.0
  3.0 + 4 * n.times.sum do |k|
    one = -one
    one / ((2 * k + 2) * (2 * k + 3) * (2 * k + 4))
  end
end

Powyższe przykłady aproksymacji liczby pi są już wiekowe. Można by pomyśleć, że przez tak długi czas nic nowego się nie pojawiło. Matematyka jednak nadal się rozwija. Technologia również pozwala nam na osiąganie lepszych wyników m.in obliczeniowych. Fakt ten wykorzystują nowe pokolenia miłośników π i jej aproksymacji.

Formuła BBP

Cóż oznacza ten tajemniczy skrót? Pochodzi on od nazwisk osób, które opublikowały swoją metodę pod koniec XX wieku: David H. Bailey, Peter Borwein i Simon Plouffe. Przedstawili oni wzór

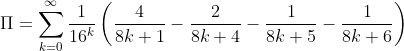
pozwalający na obliczanie w systemie szesnastkowym n-tej liczby pi bez konieczności wyliczania poprzedzających cyfr. Pozwala to na zrównoleglenie prac obliczeniowych np. na superkomputerach. Spróbujmy obliczyć π na naszym “superkomputerze”.

def approximation_pi_with_bbp_formula(n)
  denominator = 1.0
  n.times.sum do |k|
    part = 8 * k
    factor = 4.0 / (part + 1) - 2.0 / (part + 4) - 1.0 / (part + 5) - 1.0 / (part + 6)
    result = factor / denominator
    denominator *= 16
    result
  end
end

Ułamek łańcuchowy i jego zastosowanie w aproksymacji Pi

Na koniec tego artykułu wspomnimy jeszcze o jednej metodzie. Nie będzie się ona opierać na ciągach. Tym razem do aproksymacji posłuży nam ułamek łańcuchowy. Istnieje wiele ułamków łańcuchowych za pomocą, których przybliża się wartość pi. Poniżej podamy rozwiązanie przedstawione przez Thomas’a J. Pickett’a i Ann Coleman.

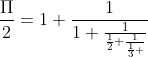
oraz jego wersję w Ruby.

class PiFromContinuedFraction
  def initialize(depth)
    @depth = depth
  end

  def calculate
    2 * (1 + 1 / continued_fraction(depth, 1))
  end

  private

  attr :depth

  def continued_fraction(depth, number)
    result = 1.0 / number
    result += 1 / continued_fraction(depth - 1, number + 1) if depth > 0
    result
  end
end

Możliwości aproksymacji jest wiele. Gdybyśmy próbowali poruszyć wszystkie z nich musiałaby powstać wielotomowa książka. 📚

Próby przybliżenia liczby pi to dobry sposób na odświeżenie wiedzy z matematyki lub jej poszerzenie. To okazja na ciekawe wykorzystanie umiejętności programistycznych i komputera. Jeśli ten ostatni odmówi współpracy - pamiętaj, zawsze jest Cieszyn i nasz serwis. Przy okazji można zwiedzić ładne okolice. 🚶